After the star-studded mystery thriller The Number 23 debuted in cinemas in 2007, many people became convinced that they were seeing the eponymous number everywhere. I was in school at that time, and some of my classmates would shudder whenever the number 23 appeared in any context. Other people became fascinated by this form of numerology because as soon as you pay more attention to a certain thing—including a number—you get the feeling that you see it too often to be purely coincidence.
For a long time, people assumed that the late mathematician John McKay might have fallen victim to this same phenomenon, known as the “frequency illusion,” or the Baader-Meinhof phenomenon. In McKay’s case, the number that captured his imagination was 196,884.
It doesn’t seem too surprising that a two-digit number such as 23 might come up repeatedly. But would a six-digit figure do so? McKay came across this number by chance in 1978 when he was looking through a paper in a mathematical field that was not his specialty. He was working in geometry and was studying the symmetry of figures. That day, however, he was looking at results from number theory, which deals with the properties of integers such as prime numbers. He came across a sequence of numbers that started with the value 196,884.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
This figure sounded familiar to McKay. He had previously worked on a mathematical structure—still hypothetical at the time—known as the monster. This strange algebraic structure was intended to describe the symmetries of a geometric object that lives in 196,883 dimensions (only one fewer than the number 196,884). And because a one-dimensional point fulfills every symmetry anyway, the monster can also describe its symmetrical properties. So McKay found the number 196,884 again in an extraordinary way. He added the first two dimensions in which mathematicians believed the monster’s symmetry applied: 196,883 + 1 = 196,884.
Does that sound far-fetched? Others thought so, too. Experts paid little attention to McKay’s result. After all, a structure such as the monster contains a number of numbers, as does the consequence from number theory that McKay had associated with it. “If you have a whole lot of numbers, then a few of them are going to be roughly the same as each other just by coincidence,” said mathematician Richard Borcherds, who has made major contributions to the field, in an explanatory YouTube video.
But McKay couldn’t shake the feeling that the two extremely different mathematical fields of geometry and number theory could be connected. He even reportedly wore T-shirts with the inscription “196,883 + 1 = 196,884” at conferences.
Complete Madness or a Stroke of Genius?
A short time later, mathematician John Thompson realized that there might be something to McKay’s suspicions after all. He succeeded in linking the next higher dimension, in which an object follows the symmetries of the monster, with the next member of the mysterious sequence of numbers from number theory. The dimension is 21,296,876. The values differ—but if you add up all the monster dimensions as before (1 + 196,883 + 21,296,876), the result is 21,493,760.
That was surprising because, as you may recall, when McKay first spotted 196,884, he was looking at a special sequence in number theory. The second number in that sequence is 21,493,760—Thompson’s result. In other words, it began to seem that there really could be a link between two seemingly unrelated areas of mathematics.
At this point the math community began to get curious. Maybe McKay was right after all—even if that sounded totally absurd. What could this strange structure, which described symmetries of unimaginable objects and had not even been fully constructed, have to do with number theory?
By 1979 evidence was mounting that other numbers and dimensions seemed to follow this unexpected pattern. Mathematicians John Conway and Simon Norton finally published a paper entitled “Monstrous Moonshine,” in which they set out the conjecture of a connection between geometry and number theory. “They called it moonshine because it appeared so far-fetched,” said number theorist Don Zagier of the Max Planck Institute for Mathematics in Bonn, Germany, to Quanta Magazine in 2015.
And indeed, there was likely very little hope of ever proving this moonshine conjecture. Quite apart from the fact that there was no indication that the two distant mathematical areas were connected, it was not even completely clear whether the monster really existed.
The Monster in the Moonlight
The monster was a theoretical prediction of group theory, an area of geometry that deals with the symmetrical properties of objects. In the 1970s mathematicians began to create a kind of periodic table of groups: they wanted to find the “atoms” of finite symmetries. According to this way of thinking, every finite group can be represented by a combination of these atoms. After decades of research, the geometers finally seemed to have reached their goal. Unlike the chemical elements, there are an infinite number of “finite simple groups,” but almost all can be divided into 18 categories, the arrangement of which is reminiscent of the periodic table. In addition, the experts came across a total of 26 outsiders that do not fit into these 18 classes.
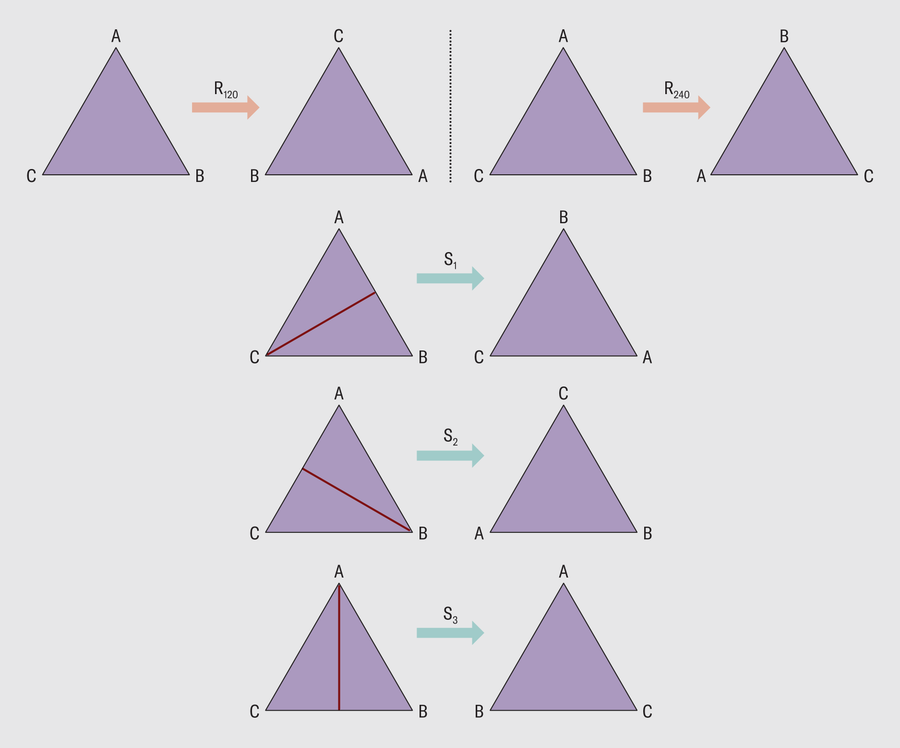
The symmetries of a triangle form a finite group. Credit: Spektrum der Wissenschaft/Manon Bischoff, restyled by Amanda Montañez
The first of these outliers was the “monster,”which mathematicians Bernd Fischer and Robert Griess predicted in 1973. The name comes from the sheer size of this group: it contains more than 8 x 1053symmetries. For comparison, the symmetry group of a 20-sided “D20” die (an icosahedron) contains 60 symmetries, meaning 60 possible transformations (rotations or reflections) can be carried out without changing the orientation of the D20.
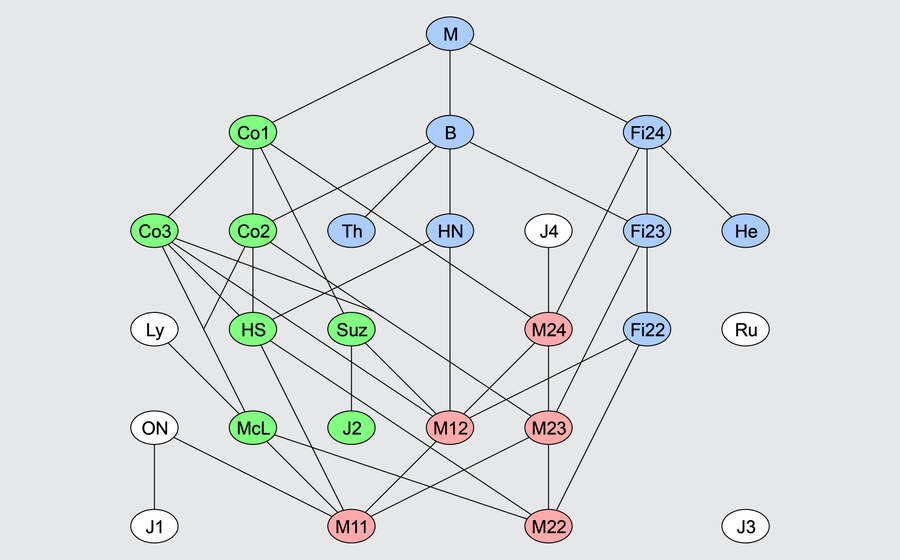
Some of the red, green and blue sporadic groups are related to one another. The white sporadic groups are considered outsiders. Credit: Drschawrz/Wikimedia Commons(CC BY-SA 3.0)
Because of its sheer size, the monster presented mathematicians with massive challenges. “Most people thought it was going to be hopeless to construct it since much, much, much smaller groups required computer constructions at that time,” explained Borcherds in his YouTube video. Meanwhile even powerful computers struggle with a structure consisting of 8 x 1053 elements.
Yet this pessimistic forecast ultimately proved wrong. In 1980 Griess constructed the monster and thus proved its existence—without the help of computers.
A Sine Function on Steroids
Number theory is mostly about integers, which seems quite simple at first glance. But to investigate the relationships between them, experts resort to complicated concepts, such as so-called modular forms. These are functions f(z) that are extremely symmetrical. As with the sine function, you only need to know a specific section of a modular form to know what it looks like everywhere else.
“Modular forms are something like trigonometric functions, but on steroids,” mathematician Ken Ono told QuantaMagazine.
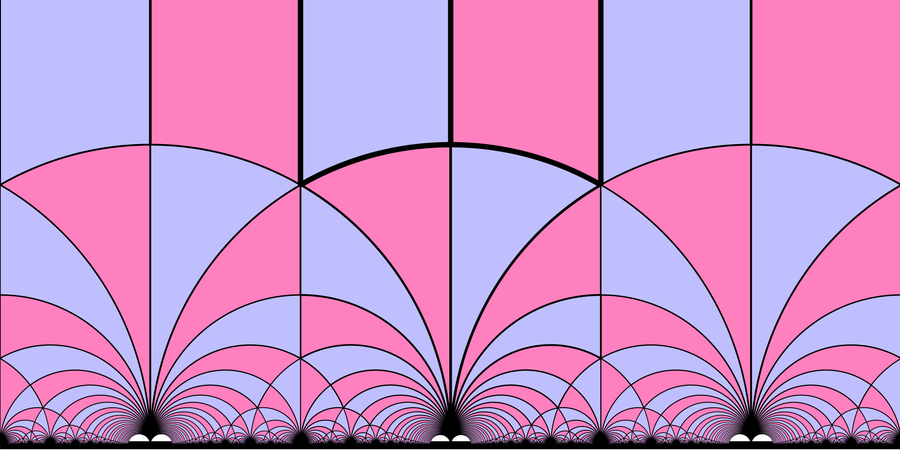
Colorful modular forms include moduli space, shown here, a geometric space whose points correspond to fixed algebro-geometric objects. Credit: Neozhaoliang/Wikimedia Commons(CC BY-SA 4.0)
Nevertheless, they play an extremely important role in mathematics. Andrew Wiles of the University of Oxford used them, for example, to prove Fermat’s theorem, and Maryna Viazovska of the Swiss Federal Institute of Technology in Lausanne used them to find the densest sphere-packing arrangement in eight spatial dimensions. Because modular forms are so complicated, however, they are often approximated by an infinitely long polynomial, such as:
f(q) = (1⁄q) + 744 + 19,688q + 21,493,760q2 + 864,299,970q3 + …
The prefactors in front of the variable q form a number sequence with interesting properties from a number-theoretical perspective. McKay associated this sequence of numbers with the monster.
A Surprising Link
Borcherds first heard about the moonshine conjecture in the 1980s. “I was just completely blown away by this,” he recalled in an interview with YouTuber Curt Jaimungal. Borcherds was sitting in one of Conway’s lectures at the time and learned that number theory and group theory could be mysteriously connected. The subject never let go of him. He began to search for the suspected connection until he found it. In 1992 he published his groundbreaking result, for which he received a Fields Medal, one of the highest awards in mathematics, six years later. His conclusion: a highly speculative area of physics, string theory, could provide the missing piece of the puzzle between the monster and the sequence of numbers.
String theory attempts to unite the four fundamental forces of physics (electromagnetism, strong and weak nuclear forces and gravity). Instead of relying on particles or waves to make up the basic building blocks of the universe, as in conventional theories, string theory involves one-dimensional structures: tiny threads vibrate like the strings of an instrument and thus generate the familiar particles and interactions that we perceive in the universe.
Borcherds knew that string theory was based on many mathematical principles related to symmetries. As it turns out, moduli also play a role. When the tiny threads are closed and move through spacetime in a wobbly manner, their track forms a two-dimensional tube. This structure has the same symmetry as modular shapes—regardless of how the thread oscillates.
The type of string theory that Borcherds investigated can only be mathematically formulated in 25 spatial dimensions. Because our world consists of only three visible spatial dimensions, however, string theorists assume that the remaining 22 dimensions are rolled up into tiny spheres or doughnut-shaped tori. But the physics depends on their exact shape: a string theory in which the dimensions are rolled up as cylinders provides different predictions than one in which they form a sphere. In order to describe the particles and their interactions in a way that fits our world, physicists have to find the right “compactification” in their calculations.
Borcherds rolled up 24 dimensions into a 24-dimensional doughnut surface and discovered that the associated string theory had the symmetry of the monster. The fact that only one free spatial dimension remained did not bother him. After all, he was interested in the mathematical properties of the model and not in a physical theory that describes our world.
In this constructed world, the threads swing along the 24-dimensional doughnut. The dimensions of the monster count all the ways in which a thread can vibrate at a certain energy. So at the lowest energy, it only vibrates in one way; at the next highest energy, there are already 196,883 different possibilities. And the trace that the thread leaves behind has the symmetry of a modular shape.
Borcherds had thus proven the connection between the monster group and a modular form. And it was not to remain the only such case: in the meantime, mathematicians have been able to connect other finite groups with other modular forms—and there, too, string theory provides the link. So even if it turns out that the speculative theory is not suitable for describing our universe, it can still help us discover completely new mathematical worlds.
This article originally appeared in Spektrum der Wissenschaft and was reproduced with permission.
