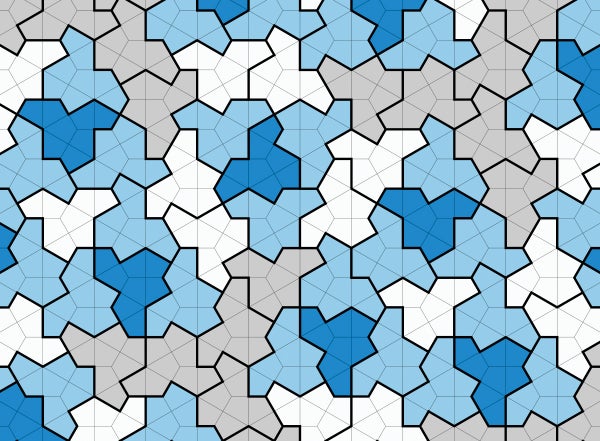
David Smith, a math hobbyist in Yorkshire, England, has discovered a 13-sided shape that eluded mathematicians for decades. The craggy, hatlike shape is called an “einstein,” based on the German for “one stone.” If you used einstein-shaped tiles to cover your bathroom floor—or any flat surface, even if infinitely large—they would fit together perfectly but never form a repeating pattern. For decades mathematicians have been hunting for tile shapes like these that can form only nonrepeating arrangements, called aperiodic tilings. They started with sets of many different tiles: the first set, discovered in 1964, required 20,426 distinct tiles, which was later simplified to 103. By 1974 mathematician Roger Penrose had found two tile shapes that, when combined in a mosaic, never formed a repeating pattern.
But was it possible to form an aperiodic tiling with tiles of only one shape—the hypothetical einstein? Doris Schattschneider, a retired mathematician affiliated with Moravian University with expertise in tessellations, had been skeptical about the likelihood of a true einstein ever being discovered. “That's why it was so startling that not only was this found, but it's such a simple tile,” she says. “To me, it's a total anomaly.” The tile Smith discovered in November 2022, while he was experimenting with different shapes using a software called PolyForm Puzzle Solver, was astonishing in its elegance. Made up of right-angled kites, it was nothing like the gnarly, complicated kind of shape many mathematicians would have predicted.
Smith e-mailed Craig Kaplan, a computer scientist at the University of Waterloo in Ontario, who recognized the shape's potential. Although the mosaic it created seemed not to have a repeating pattern, the duo needed to mathematically prove it never would—even if the mosaic were infinitely large. They enlisted software developer Joseph Samuel Myers and University of Arkansas mathematician Chaim Goodman-Strauss, who had both worked with tiling and combinatorics in the past.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
The researchers used two methods to prove they had a genuine einstein on their hands. First, they showed that the hatlike tiles, when arranged together, formed four specific kinds of shapes. Adding more tiles forms even bigger versions of those same shapes, or “supertiles;” the more tiles added, the bigger the supertiles become. Mathematicians have proved that this hierarchical structure means the tiling can't be split into repeating sections and thus must be aperiodic. For the second proof, the team invented a new method that could compare the hat tilings with the nonperiodic tilings of better-known shapes called polyiamonds. In the process, the team also showed that one could make an infinite number of similar einsteins by tweaking some of the sides' lengths.
Even with these proofs, mathematicians haven't yet formulated a broader theory for what makes this simple hat shape so special. “This is still very mysterious,” says mathematician Rachel Greenfeld of the Institute for Advanced Study in Princeton, N.J. There may be more classes of einstein tiles out there, waiting to be discovered, but the geometric hat isn't revealing any clues, says Marjorie Senechal, a retired mathematician affiliated with Smith College: “These things you stumble upon.”
Editor’s Note: A previous version of this story appeared online with the title “Newfound Mathematical ‘Einstein’ Shape Creates a Never-Repeating Pattern.”