Open your favorite social media platform and note how many friends or followers you have. Specifically, note the first digit of this number. For example, if you have 400 friends, the leading digit is 4, and if you have 79, it's 7. Let's say we asked many people to do this. We might expect responses across the board—common intuition suggests that friend counts should be somewhat random, and therefore their leading digits should be, too, with 1 through 9 showing up equally. Strangely, this is not what we would find. Instead we would see a notable imbalance with nearly half of the friend counts beginning with 1 or 2 and a paltry 10 percent beginning with 8 or 9. Remember, this isn't about having more or fewer friends; 1,000 friends is way more than eight.
This bizarre overrepresentation of 1 and 2 extends beyond friends and followers to likes and retweets and well beyond social media to countless corners of the numerical world: national populations, river lengths, mountain heights, death rates, stock prices, even the diverse collection of numbers found in a typical issue of Scientific American. Not only are smaller leading digits more common but they follow a precise and consistent pattern.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
If all digits were represented equally, then they would each appear one ninth (about 11.1 percent) of the time. Yet in an uncanny number of real-world data sets, an astonishing 30.1 percent of the entries begin with a 1, 17.6 percent begin with a 2, and so on. This phenomenon is known as Benford's law. The law holds even when you change the units of your data. Measure rivers in feet or furlongs, measure stock prices in dollars or dinars—any way you measure, these exact proportions of leading digits persevere. Although mathematicians have proposed several clever reasons for why this pattern might emerge, its sheer ubiquity evades a simple explanation.
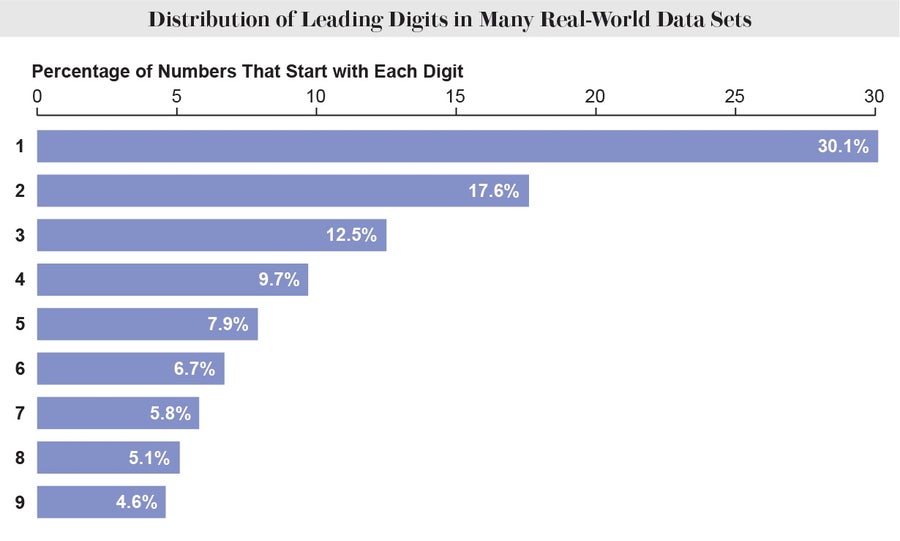
Credit: Amanda Montañez; Source: “Note on the Frequency of Use of the Different Digits in Natural Numbers,” by Simon Newcomb in American Journal of Mathematics, Vol. 4, No. 1; 1881 (data)
As it happens, Benford was not the first to discover Benford's law. Before calculators, people outsourced hairy arithmetic to reference books called logarithm tables. In 1881 astronomer Simon Newcomb noticed that early pages of logarithm tables, which correspond to numbers beginning with 1, were grubby and worn compared with the later pages. He deduced that smaller leading digits must be more common in natural data sets, and he published the correct percentages. Physicist Frank Benford made the same observation in 1938 and popularized the law, compiling more than 20,000 data points to demonstrate its universality.
The law has been used to put people behind bars. Financial adviser Wesley Rhodes was convicted of defrauding investors when prosecutors argued in court that his documents did not accord with the expected distribution of leading digits and therefore were probably fabricated. The principle later helped computer scientist Jennifer Golbeck uncover a Russian bot network on Twitter. She observed that for most users, the number of followers that their followers have adheres to Benford's law, but artificial accounts significantly veer from the pattern. Examples of Benford's law being applied to fraud detection abound, from Greece manipulating macroeconomic data in its application to join the eurozone to vote rigging in Iran's 2009 presidential election. The message is clear: organic processes generate numbers that favor small leading digits, whereas naive methods of falsifying data do not.
Why does nature produce a dearth of 9s and a glut of 1s? First, it's important to state that many data sets do not conform to Benford's law. Adult heights mostly begin with 4, 5 and 6 when measured in feet. A roulette wheel is just as likely to land on a number beginning with 2 as on one with 1. The law is more likely to apply to data sets spanning several orders of magnitude that evolve from certain types of random processes.
Exponential growth is a particularly intuitive example. Imagine an island that is initially inhabited by 100 animals, whose population doubles every year: after one year there are 200 animals, and after two years there are 400. Already we notice something curious about the leading digits. For the entire first year the first digit of the population of the island was a 1. In the second year population counts spanned the 200s and 300s in the same length of time, leaving less time for each leading digit to reign. This continues with 400 to 800 in the third year, when the leading digits retire faster still.
The reason is that growing from, say, 1,000 to 2,000 requires doubling, whereas growing from 8,000 to 9,000 is only a 12.5 percent increase, and this trend resets with each fresh order of magnitude. There is nothing special about the parameters we chose in the island example. We could begin with a population of 43 animals and grow by a factor of 1.3 per year, for example, and we would see the same exact pattern of leading digits. Almost all exponential growth of this kind will tend toward Benford's law.
The law's stubborn indifference toward units of measure gives another hint as to why the pattern is so common in the natural world. River lengths follow Benford's law whether we record them in meters or miles, whereas non-Benford-compliant data such as adult heights would radically change their distribution of leading digits when converted to meters because nobody is four meters tall. Remarkably, Benford's law is the only leading digit distribution that is immune to such unit changes.
We can think of changing units as multiplying every value in our data set by a certain number. For example, we would multiply a set of lengths by 1,609.34 to convert them from miles to meters. Benford's law is actually resilient to a much more general transformation. Taking Benford-compliant data and multiplying each value by a different number (rather than a fixed one such as 1,609.34) will leave the leading digit distribution unperturbed. This means that if a natural phenomenon arises from the product of several independent sources, then only one of those sources must accord with Benford's law for the overall result to. Benford's law is cannibalistic, much in the same way that a single zero in a bunch of numbers being multiplied together makes the result zero.
These explanations don't explain why the diverse collection of numbers plucked from an issue of Scientific American would adhere to Benford's law. These numbers don't grow exponentially, and we're not multiplying them together. Mathematician Ted Hill discovered what many consider to be the definitive proof of the leading-digit law. He argues that if you pick a bunch of random numbers from a bunch of random data sets, they will tend toward Benford's law. In other words, although countless data sets show Benford's pattern, the most reliable way to manifest it is to pull numbers from varying sources, such as those we see in a newspaper.
I've spent a lot of time thinking about Benford's law, and it still surprises me how often it shows up. Pay attention to the numbers you encounter in your daily life, and you might begin to spot examples of it.
